圓周率

作者∕徐任宏

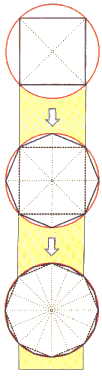
「好哇！竟然把我勉勵你的話，拿來教訓我！」我故作生氣地說。

「哈哈！這就是我厲害的地方呀！你看喔，如果把正八邊形再變成正十六邊形……」怡倩繼續在紙上畫著。「就會越來越像圓喔！很神奇吧！」

「嗯！的確很神奇！那你有什麼心得呢？」

「沒有呀，我只是覺得很好玩而已！」

「真可惜！不然你就和古代的數學家一樣厲害了！」

「啊？為什麼？為什麼？」

「你知不知道圓周率是什麼？」

「知道呀！圓周率等於三點一四嘛！」

「哎呀，我不是問你圓周率等於多少，我是問你『圓周率是什麼？』」

「好，圓周率是什麼？」

「圓周率就是……，咦，怎麼變成你問我了？」

「啊！被你發現了！」

「算了！我看還是公佈答案吧：圓周率就是圓周長和直徑的比值。」

「這我早就知道了呀！」

「那你知不知道數學家是怎樣求出圓周率的呢？」

「那還不簡單，拿一把尺量一量圓周長和直徑，再相除就好了呀！」

「這個方法當然可以求出圓周率大約的值，不過，這不是正確的科學態度喔！因為在量長度的過程中，一定會有誤差產生，我們所得到的結果也就不可能很精確。在三千多年前，中國周朝的時候，認為圓周長和直徑的比是三比一，也就是說，那個時候的圓周率等於三，很有可能就是運用你所說的方法算出來的喔！」

「後來呢？」

「後來，歷代許多數學家，像西漢的劉歆、東漢的張衡，都分別提出新的數值。不過，真正求出比較精確圓周率的，是三國時代的劉徽，而他所用的方法，其實就是你剛剛所發現的喔！」

「真的呀？」

「嗯！劉徽把這個方法叫做『割圓術』。他發現：當圓內接正多邊形的邊數不斷增加以後，多邊形的周長會越來越逼近圓周長，而多邊形的面積也會越來越逼近圓面積。於是，劉徽利用正多邊形面積和圓面積之間的關係，從正六邊形開始，逐步把邊數加倍：正十二邊形、正二十四邊形，正四十八邊形……，一直到正三○七二邊形，算出圓周率等於三點一四一六。」

「天啊！正三○七二邊形！他是怎麼算的呀？」

「在中國古時候，數學家利用一種竹片做成的『算籌』，擺放在地上代表數字進行運算，不但麻煩而且辛苦呢！」

「那如果跑進來一隻貓，把竹片弄亂了怎麼辦？」

「那就只好重來囉！」

「還真有耐性呢！」

「這也是一種科學的態度呀！不怕麻煩也不怕累！不過，中國古時候，在圓周率方面貢獻最大的科學家，是南朝宋國的祖沖之。」

「嗯！小祖嘛，我知道他！」

「這位祖沖之先生可不簡單喔！他在劉徽研究的基礎上，進一步地發展，經過既漫長又煩瑣的計算，一直算到圓內接正二四五七六邊形，而得到一個結論：圓周率的值介於3.1415926和3.1415927之間；同時，他還找到了圓周率的約率：22∕7、密率：355∕113。這些研究結果，都領先了西方的數學家一千多年呢！」

「好了不起喔！」

「是呀！雖然現在電腦發達，可以在很短的時間之內，就求出圓周率小數點後面幾千、幾萬個位數；但是，古人們在完全依靠人工計算的情況下，為了追求科學真理，義無反顧地獻身其中的熱情與毅力，更值得我們學習與敬佩喔！」

「嗯！」

我希望二寶看完這篇故事能有一點基本概念!